Os gráficos (4), (5) e
(6) novamente mostram a performance dos
métodos em termos de obter soluções
aproximadas da solução analítica de
problemas de valor inicial, mas agora
para um PVI cuja solução analítica
fornece uma função com uma região
crítica, onde os métodos podem se
mostrar inadequados, o PVI2. O intervalo
estudado foi [-3,3] onde a função
solução analítica do PVI2 tem um pico,
isto é, uma curva mais fechada em
relação as curvas apresentadas pela
função anterior.
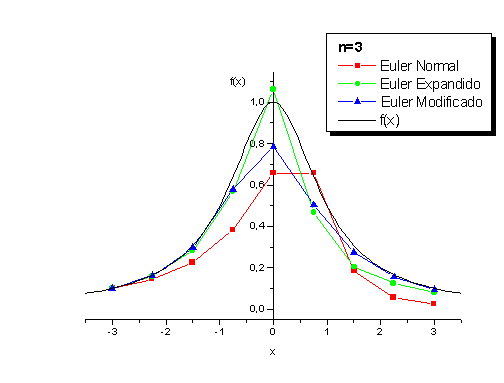
Gráfico 4.
Comparação entre os Métodos de Euler,
Euler Expandido e Euler
Modificado para o PVI2 (y' =
-2xy/(1+x2)), y(-3)=0,1)
com n=3 (8 iterações).
O gráfico (4)
mostra, para 8 iterações, as soluções
obtidas na aplicação dos métodos de
Euler Normal, Euler Expandido e Euler
Modificado para o PVI2. Observa-se,
que para o tamanho de passo dado neste
intervalo pelos métodos, nenhum deles
demonstrou-se satisfatório para
descrever uma aproximação para a
solução exata. Mesmo assim, com uma
aproximação grosseira, pode-se afirmar
que neste caso, o método de Euler
Expandido demonstrou, durante o
intervalo [-3,1] (compreendendo a
região crítica) uma solução um pouco
melhor do que a dos outros dois
métodos. Isto revela que o terceiro
termo da série de Taylor foi
importante; claro, sendo o valor de n
pequeno, e consequentemente um valor
de h significativo, o termo  é
representativo para a solução
aproximada, isto é, o erro de
truncamento para esta situação se
destaca perante os outros erros
possíveis. Agora continuando para o
resto do intervalo, [1,3], o método de
Euler Expandido torna-se menos preciso
que o Euler Modificado revelando que o
erro de propagação começa a superar o
erro de truncamento.
Gráfico 5.
Comparação entre os Métodos de Euler,
Euler Expandido e Euler
Modificado para o PVI2 (y' =
-2xy/(1+x2)), y(-3)=0,1)
com n=5 (32 iterações).
O gráfico (5),
quando o número de iterações aumenta
para 32 iterações, a situação melhora
bastante, onde até mesmo na região
crítica os métodos já tem uma boa
aproximação para a solução exata do
PVI2. Somente o método de Euler normal
é que ainda não fornece bons
resultados, onde nota-se um desvio da
curva de f(x), solução de PVI2.
Gráfico 6 .
Comparação entre os Métodos de Euler,
Euler Expandido e Euler
Modificado para o PVI2 (y' =
-2xy/(1+x2)), y(-3)=0,1)
com n=7 (128 iterações).
Observando o gráfico
(6), já não consegue-se distinguir
graficamente o traçado dado pela
função solução analítica do PVI2 e as
curvas traçadas pelas soluções
numéricas obtidas pelos métodos de
Euler Expandido e Modificado. Enquanto
que o desvio por parte da solução
alcançada pelo método de Euler Normal
ainda é bem perceptível na região
crítica. Isto revela que para se obter
uma solução mais apurada deste PVI por
este método seria necessário um número
maior de iterações.
Na observação dos três
últimos gráficos:(4), (5) e (6),
percebe-se que quando há uma região onde
os valores das derivadas nos pontos
mudam bruscamente, característico de
curvas mais fechadas, os métodos
encontram uma maior dificuldade para
encontrar aproximações para a solução
exata. Verifica-se, na resolução do
PVI2, maiores desvios, seja para n=3, 5
ou 7, no intervalo [-1,1] onde aparece
uma curva acentuada, sendo que para o
resto do intervalo, onde o traçado é
mais suave, as aproximações são
melhores. |
