|
O método
de Euler Simples é utilizado para
resolução de equações diferenciais
ordinárias (EDOs), principalmente
aquelas na qual a solução analítica é
difícil ou até mesmo impossível de
serem obtidas.
Este
método tem seu princípio na série de
Taylor (Equação 1), que para este caso
específico, é truncada no segundo
termo (Equação 2).
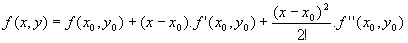 (1) (1)
O valor (x
– xo) é igual a (h), que é
chamado de passo. Este passo é
calculado da seguinte forma:
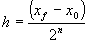 , onde: , onde:
xf
é o intervalo final, na qual se
deseja obter a solução;
n é um
número aleatório que decidirá qual
será o tamanho do passo, este tem
uma enorme influência na precisão
do método e será discutido
posteriormente.
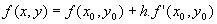 (2)
(2)
A essência
deste método é muito simples, que
resume-se a tangenciar a função passo
a passo, de modo a poder descrevê-la.
O artifício matemático usado para este
é a derivada.
Pela
equação (2) podemos ver que a única
incógnita é f (x,y), pois f(xo,
yo) é a condição inicial
imposta pelo problema, h é o valor do
passo, e f ’(xo, yo)
é a EDO dada também pelo problema.
A
descrição geométrica do método está
esquematizada na figura 1, claro que
de forma exagerada para ser possível
sua visualização.
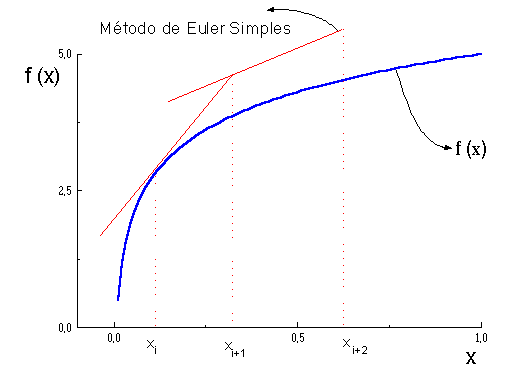
Figura 1 - Descrição
geométrica
do método de Euler Simples
Este
método acarreta erros, que serão
mostrados e discutidos no desenrolar
deste trabalho. Estes erros são
ocasionados primeiro pelo truncamento
da série de Taylor no segundo termo,
segundo pelos arredondamentos
efetuados nas operações matemáticas
realizadas pelo computador e em
terceiro pela propagação dos erros,
que são cumulativos neste sistema,
como pode ser visto pela figura 1.
Em função
desses problemas citados acima,
originaram dois novos métodos, que
surgiram para minimizar esses erros.
Eles são chamados de Euler Expandido e
Euler Modificado, que serão discutidos
a seguir.
|