|
Para
analisar as vantagens e desvantagens,
e/ou ainda, as condições para se
utilizar um ou outro método,
construiu-se uma série de gráficos
ilustrativos, de modo que as
diferenças da adoção dos métodos
ficasse bem representada.
Neste
estudo comparativo, procurou-se
contemplar diferentes funções, isto é,
com comportamentos analíticos
diferentes, o número de iterações
adequado a ser utilizado pelos métodos
numéricos a procura de uma solução
aproximada, e o erro cometido pela
adoção dos métodos.
Uma
primeira análise realizada sobre os
métodos de Euler e suas variantes foi
a utilização de problemas de valor
inicial (PVIs) de primeira ordem cujas
soluções analíticas são conhecidas, e
dadas por funções com curvas de
caráter distintos. Foi observado as
soluções aproximadas encontradas pelos
métodos para diferentes tamanhos de
passo, ou números de iterações
efetuado. Esta análise é baseada nos
gráficos (1), (2), (3), (4), (5) e
(6).
Os PVIs,
com suas respectivas soluções
analíticas, utilizadas foram as
seguintes:
- PVI1
 solução
analítica : 
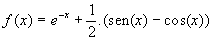
- PVI2
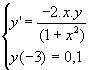 , solução
analítica: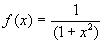 
É importante
ressaltar que o valor da variável 'n'
representa uma parcela considerável no
cálculo do tamanho do passo a ser
utilizado pelos métodos, já que este
último é dado por:
 (1)
onde h é o
tamanho do passo, [a,b] é o intervalo
de interesse de solução numérica. O
número de iterações a ser efetuado
pelos métodos é baseado no valor de
'n'. Pela equação (1) o número de
iterações é da ordem de 2n.
|
