Nos gráficos (1), (2) e (3) estão plotados: a função derivada da resolução analítica do PVI1() e as soluções aproximadas encontradas para o PVI1 no intervalo [0,4]. O que diferencia os três gráficos é o valor de 'n' (alterando o número de iterações) utilizado na obtenção da solução numérica. É importante notar que o comportamento da solução analítica do PVI1 no intervalo dado, é bem comportado, com curvas suaves.
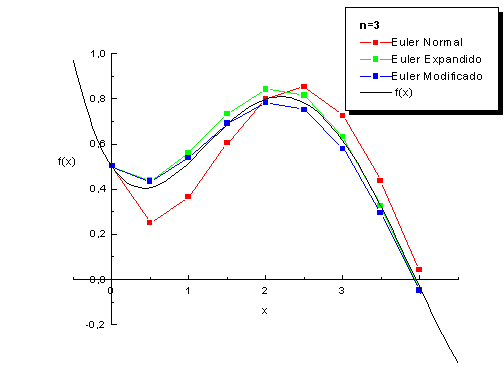Gráfico 1. Comparação entre os Métodos de Euler, Euler Expandido e Euler
Modificado para o PVI1 (y' = sen(x) - y, y(0)=0,5) com n=3 (8 iterações).

 

No gráfico (1), o número de iterações realizado no intervalo foi de 8 iterações (n=3 ® 2³ ). Verificou-se que para este tamanho de passo os métodos encontram aproximações grosseiras, e não conseguem acompanhar as curvas, ou melhor, o traçado da função solução analítica. Mesmo assim, já percebe-se que os métodos de Euler Expandido e Modificado fornecem melhores resultados que o método de Euler Normal, como era de se esperar.

No gráfico (2), onde o número de iterações aumenta para 32 iterações (n=5 ® 2⁵ ), a solução numérica começa a representar as curvas da solução do PVI1 de maneira mais adequada. Note que um aumento de 8 para 32 iterações foi suficiente para se obter resultados significativamente melhores dentro do intervalo de interesse para os três métodos. Ainda é notável um desvio maior do método de Euler Normal em relação aos outros dois métodos.  

Gráfico 2. Comparação entre os Métodos de Euler, Euler Expandido e Euler Modificado para o PVI1 (y' = sen(x) - y, y(0)=0,5) com n=5 (32 iterações).

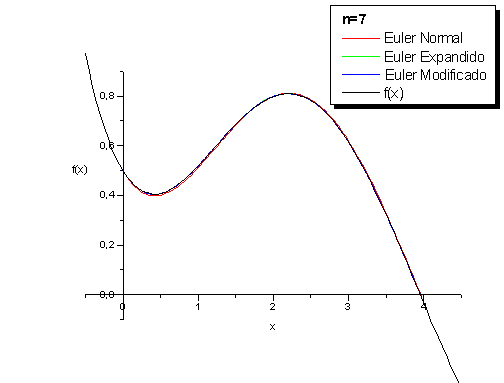
Gráfico 3. Comparação entre os Métodos de Euler, Euler Expandido e Euler
Modificado para o PVI1 (y' = sen(x) - y, y(0)=0,5) com n=7 (128 iterações).

Aumentando o número de iterações para 128 iterações(n=7 ® 2⁷ ), representado pelo gráfico (3), percebe-se, pelo menos graficamente, que não há mais diferença entre o traçado dado pela solução exata e pela solução aproximada dos métodos de Euler Expandido e Euler Modificado. Quanto ao Euler Normal, apesar de ter seu traçado semelhante ao traçado da função f(x), os desvios para os pontos no início do intervalo ainda podem ser visualizados.

Esta última observação chama a atenção para que neste PVI, a região mais problemática, apesar de saber da existência dos erros de propagação, é a região inicial do intervalo onde se vê maiores desvios entre as soluções numéricas e a exata nos três gráficos: (1), (2) e (3).